1. Verificatie van het fysische principe van de kernformule
Wet van behoud van massa
Alle formules zijn gebaseerd op de fysieke aard van m=ρ×V (massa = dichtheid × volume)
Dichtheidswaarde
Theoretische dichtheid van zuiver aluminium: 2.698 kg/m³ (20℃)
De geschatte waarde van 2.700 kg/m³ is redelijk voor industriële berekeningen (fout < 0,1%)
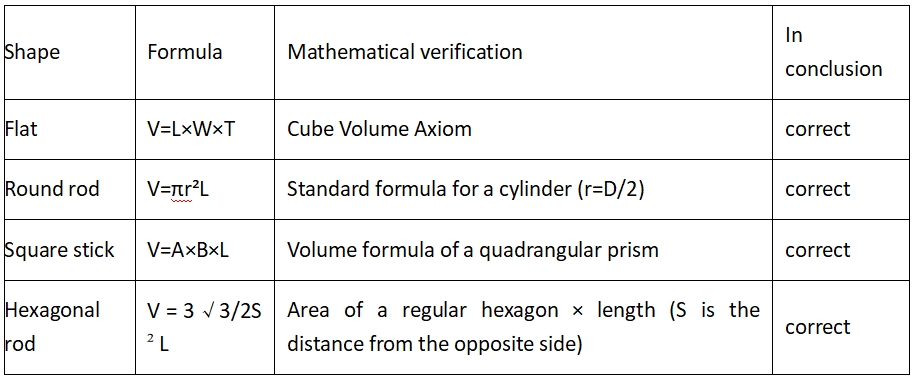
2. Verificatie van de nauwkeurigheid van geometrische formules
2.1. Standaard geometrische volumeformule
Beperkingen van de formule voor vierkante buizen:
Dit is waar wanneer de wanddikte van de buis uniform is en de binnenhoek een rechte hoek is (de werkelijke vierkante buis heeft een afgeronde overgang en de theoretische fout is ongeveer 1-3%)
3. Verificatie van de consistentie van het eenheidssysteem
Onderzoek naar risicopunten bij berekening van meerdere eenheden
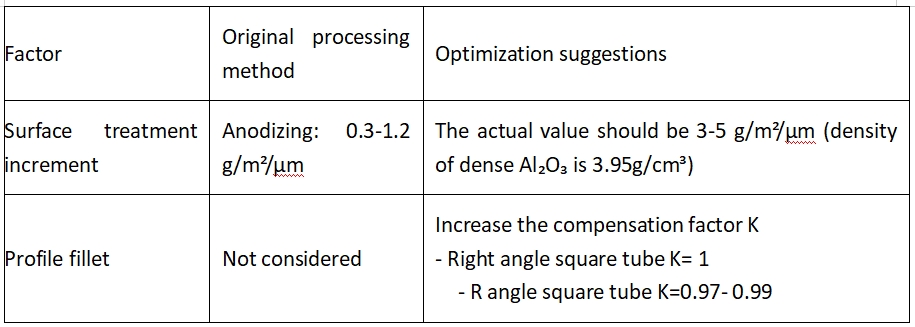
4. Wijziging van de technische geschiktheid
4.1. Compensatie voor niet-ideale factoren
4.2. Kwantificering van de impact van tolerantie
Diktetolerantie ±10% → Gewichtsafwijking ±(8% ~ 12%) (dunwandige onderdelen zijn gevoeliger)
Oplossing: W werkelijk = W theoretisch × (1 + Δt / t) (Δt : dikteafwijking)
5. Randvoorwaardetest
Extreem geval verificatie:
Scenario met dichtheidsanomalie
7xxx-legering (7075): Gemeten dichtheid 2,810 g/cm³ → Als per ongeluk 2,7 g/cm³ wordt gebruikt, is de fout +4,1%.
Formuletabel
4t(A + B)- 4t² is een standaard technische berekening die wordt berekend door de omtrek van het profiel te vermenigvuldigen met de wanddikte en vervolgens de vier hoeken ervan af te trekken.
Rekenvoorbeeld:
1.6061 aluminium plaat(1000 × 500 × 10 mm, lengte 2 m): B = 1000 × 500 × 2 × 0,0027 = 27 kg
2.7075 ronde buis(buitendiameter 50 mm, wanddikte 3 mm, lengte 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Vierkante buis(40×40×2mm, lengte 3m): B = [2×2×(40+40-4)×3]×0,0027×0,98 ≈ 2,42 kg
Aanbevolen workflow
1. Selecteer dichtheid → 2. Meet de werkelijke grootte → 3. Selecteer compensatiefactor → 4. Bereken met formule
Plaatsingstijd: 17 juni 2025